Questão: Uma carreta sobe uma estrada cuja inclinação em relação à horizontal é de 30°, a uma velocidade de 40km/h. A força resistiva é igual a 0,75 do peso da carreta. Que velocidade teria a mesma carreta se descesse a estrada com a mesma potência?
Resposta:
Generalizando, vou chamar o ângulo de Θ e o coeficiente da orça resistiva de ψ.
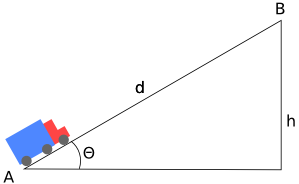
Figura 1 – A subida
Essa força resistiva não é exatamente o atrito, porque se fosse o atrito terÃamos de calcular as componentes do peso para descobrir a normal. O trabalho exercido por essa força resistiva é igual a força ψ·m·g vezes a distância d.
Na subida:
Ea=Eb
onde
- Ea = m·v²/2 + Em
- Eb = m·v²/2 + m·g·h + ψ·m·g·d
A carreta ira de um certo ponto A para um certo ponto B com uma mesma velocidade, a inércia pode cuidar disso. Mas a carreta precisa de alguma energia para converter em energia potencial gravitacional e na energia gasta pelo atrito. Essa energia vamos chamar de Em, a energia do motor. A carreta já parte com essa energia guardada para ser transformada em outras formas de energia. Podemos ver isso como o combustÃvel do veÃculo. Note que nenhuma energia aparece ou se perde.
Igualando as duas equações temos:
- m·v²/2 + Em = m·v²/2 + m·g·h + ψ·m·g·d
cortando a energia cinética dos dois lados e como h = d·senΘ:
- Em = m·g·d·senΘ + ψ·m·g·d
colocando d em evidência:
- Em = d·(m·g·senΘ + ψ·m·g)
A potência do motor na subida é dada pelo trabalho desenvolvido pelo motor dividido pelo tempo levado para subir do ponto A até o ponto B.
- Pm = Em/t
Como eu não tenho esse tempo eu posso dizer que o tempo é igual à distância dividida pela velocidade.
- Pm = Em/(d/v)
- Pm = Em·v/d
Substituindo Em:
- Pm = d·(m·g·senΘ + ψ·m·g)·v/d
- Pm = (m·g·senΘ + ψ·m·g)·v
- Pm = v·m·g·(senΘ + ψ)
Na descida:
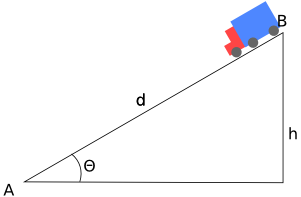
Figura 2 – A descida
Usando o mesmo raciocÃnio e notação da subida temos:
Ea=Eb
onde
- Ea = m·v²/2 + ψ·m·g·d
- Eb = m·v²/2 + m·g·h + Em
igualando as duas equações:
- m·v²/2 + ψ·m·g·d = m·v²/2 + m·g·h + Em
- ψ·m·g·d = m·g·h + Em
- Em = ψ·m·g·d – m·g·h
Como h = d·senΘ:
- Em = ψ·m·g·d – m·g·d·senΘ
- Em = d·m·g·(ψ – senΘ)
A potência do motor é dada pelo trabalho sobre o tempo:
- Pm = Em/t
Novamente não conhecemos o tempo mas sabemos que ele é a distância sobre a velocidade, que vou chamar de v linha para diferenciar da velocidade da carreta na subida:
- Pm = Em/(d/v’)
- Pm = Em·v’/d
Substituindo Em:
- Pm = d·m·g·(ψ – senΘ)·v’/d
- Pm = v’·m·g·(ψ – senΘ)
Como queremos que a potência na subida seja igual a potência na descida, igualamos as equações das potências:
- v·m·g·(senΘ + ψ) = v’·m·g·(ψ – senΘ)
- v·(senΘ + ψ) = v’·(ψ – senΘ)
- v’·(ψ – senΘ) = v·(senΘ + ψ)
- v’ = v·(senΘ + ψ) / (ψ – senΘ)
Note que nesse problema, a velocidade na descida só depende da velocidade na subida, o coeficiente da força resistiva e do ângulo Θ.
Calculando para v = 40km/h, ψ = 0,75, Θ = 30º e senΘ = 0,5.
- v’ = 40km/h·(0,5 + 0,75) / (0,75 – 0,5)
- v’ = 40km/h·1,25 / 0,25
- v’ = 200km/h
Caraleo!!! O.o
200 km/h????
é um caminhão ou um fórmula 1?
heheheh
ps.: tu faz fÃsica, é?
Éguaaaaa! Chega deu um nó nos neurônios.
Faz um tempão que não via isso. 18 anos atrás eu era bom nisso!
Alessandro, não, eu faço computação mas temos uma cadeira de fÃsica geral. Infelizmente eu não sou mais tão bom em fÃsica quanto eu era no ensino médio.
essa velocidade não teria que ser transformada em m/s?
Sim, é uma pergunta retórica. Abraços.
Muito Teórico !! A maior inclinação de uma via é de 19 graus (No mundo)