A simple gaussian elimination implemented in C.
To simplify, I hard coded the linear system
 |
10 x1 | + 2 x2 | + 3 x3 | + 4 x4 | = 5 |
| 6 x1 | + 17 x2 | + 8 x3 | + 9 x4 | = 10 | |
| 11 x1 | + 12 x2 | + 23 x3 | + 14 x4 | = 15 | |
| 16 x1 | + 17 x2 | + 18 x3 | + 29 x4 | = 20 |
into the AB float matrix.
/* * Description: Solve a hard coded linear system by gaussian elimination * Author: Silveira Neto * License: Public Domain */ #include <stdio.h> #include <stdlib.h> #define ROWS 4 #define COLS 5 /** * Linear System, Ax = B * * 10*x1 + 2*x2 + 3*x3 + 4*x4 = 5 * 6*x1 + 17*x2 + 8*x3 + 9*x4 = 10 * 11*x1 + 12*x2 + 23*x3 + 14*x4 = 15 * 16*x1 + 17*x2 + 18*x3 + 29*x4 = 20 */ float AB[ROWS][COLS] = { {10, 2, 3, 4, 5}, { 6, 17, 8, 9, 10}, {11, 12, 23, 14, 15}, {16, 17, 18, 29, 20} }; /* Answer x from Ax=B */ float X[ROWS] = {0,0,0,0}; int main(int argc, char** argv) { int row, col, i; /* gaussian elimination */ for (col=0; col<COLS-1; col++) { for (row=0; row<ROWS; line++){ float pivot = AB[row][col]/AB[col][col]; if(row!=col) { for(i=0; i<COLS; i++) { AB[row][i] = AB[row][i] - pivot * AB[col][i]; } } } } /* X = B/A and show X */ for(row=0; row<ROWS; line++) { X[row] = AB[row][ROWS] / AB[row][row]; printf("%3.5f ", X[row]); } printf("n"); return (EXIT_SUCCESS); } |
Before the gaugassian elimination, AB is
10 2 3 4 5 6 17 8 9 10 11 12 23 14 15 16 17 18 29 20
and after it is
10.00000 0.00000 0.00000 0.00000 2.82486 0.00000 15.80000 0.00000 0.00000 3.92768 0.00000 0.00000 15.85443 0.00000 3.85164 0.00000 0.00000 0.00000 14.13174 3.35329
that corresponds to
|
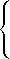
10 x1 | = 2.82486 | |||
| 15.80000 x2 | = 3.92768 | ||||
| 15.85443 x3 | = 3.85164 | ||||
| 14.13174 x4 | = 3.35329 |
The solution vector is X = (x1, x2, x3, x4). We get it by X=B/A.
The program output, X, is
0.28249 0.24859 0.24294 0.23729
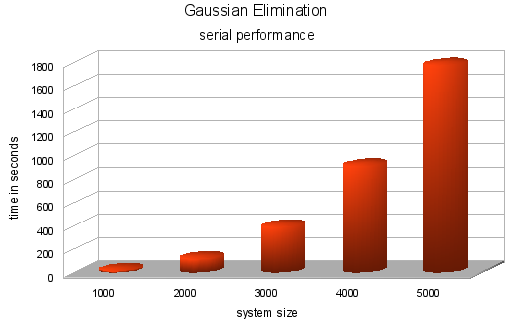
Benchmarking:
I’m this serial implementation over one node of our cluster, a machine with 4 processors (Intel Xeon 1.8 Ghz) and 1Gb RAM memory. I tried random systems from 1000 to 5000 variables and got the average time.
nice, i remember what is it now, heh.
where will you apply it??
sombriks, I also wrote a parallel version of gaussian elimination using MPI. My idea now is to benchmark them.
Hi, nice work. Just for language war, some time ago I’ve done a python version:
http://pastebin.com/f17960864
Cool! I’ve pasted here:
import sys ############# # Buggy Gauss Elimination # (Zero division is not checked) # def det(rows): v = None if len(rows) == 2: r1 = rows[0] r2 = rows[1] v = r1[0] * r2[1] - r1[1] * r2[0] else: firstRow = rows[0] aboveRows = rows[1:] subDets = [] # At time I din't know the existence of enumerate for c in range(0, len(firstRow)): subMatrix = [] for ar in aboveRows: subRow = [] for c2 in range(0, len(ar)): if c != c2: subRow.append(ar[c2]) subMatrix.append(subRow) subDets.append(det(subMatrix) * firstRow[c]) evens = [subDets[e] for e in range(0, len(subDets), 2)] odds = [subDets[e] for e in range(1, len(subDets), 2)] v = reduce(lambda x, y: x+y, evens) - reduce(lambda x, y: x+y, odds) return v #non-recursive def solveSystem(rows): if det(rows) == 0: return None zerorColumnNth = 0 solvedSystem = rows for workRowNth in range(0, len(rows)-1): for prodRowNth in range(workRowNth+1, len(rows)): workRow = solvedSystem[workRowNth] prodRow = solvedSystem[prodRowNth] mul = -prodRow[zerorColumnNth] / workRow[zerorColumnNth] newProdRow = map(lambda a, b: a + b, map(lambda x: x*mul, workRow), prodRow) solvedSystem[prodRowNth] = newProdRow zerorColumnNth += 1 return solvedSystem #recursive def solveSystem2(rows): def solveLoop(rows, workNth, prodNth, zeroColumn, nrows): if prodNth < nrows: workRow = rows[workNth] prodRow = rows[prodNth] mul = -prodRow[zeroColumn] / workRow[zeroColumn] rows[prodNth] = map(lambda a, b: a + b, map(lambda x: x*mul, workRow), prodRow) return solveLoop(rows, workNth, prodNth+1, zeroColumn, nrows) else: if workNth = 0: row = rs[nth] vt = [vals[v]*row[v] for v in range(nth+1, len(row)-1)] if len(vt) > 0: coff = -reduce(lambda a, b: a+b, vt) else: coff = 0 vals[nth] = (coff + row[len(row)-1])/row[nth] return retroLoop(rs, nth-1, vals) return vals nrows = len(rows) return retroLoop(rows, nrows-1, [0 for i in range(0, nrows)]) if __name__ == '__main__': try: f = open(sys.argv[1], 'r') except IOError, msg: print(msg) sys.exit(1) rows = [] for line in f: if line != '\n': atoms = line.split(' ') r = [] for a in atoms: r.append(float(a)) rows.append(r) f.close(); maxColumn = 0 for r in rows: cs = len(r) if cs > maxColumn: maxColumn = cs for r in rows: cs = len(r) if cs != maxColumn: print("Matrix nao quad") sys.exit(1) ss = solveSystem2(rows) r = retroSub(ss) print(r) ############## # Sample input file: # # 10 2 3 4 5 # 6 17 8 9 10 # 11 12 23 14 15 # 16 17 18 29 20 # Should output: # [0.28248587570621464, 0.24858757062146891, 0.24293785310734467, 0.23728813559322035]I’ll do just a observation: if A and B are matrixes, the operation B/A doesn’t exist. You have to do B*inv(A), in fact if C = inv(A) then C(i,j) = 1/A(i,j) because A is a digonal matrix.
Merry Christmas for everyone!!!
God will help us more in next year!
I’m not the only one who finds amusement in the irony of the C version being shorter and clearer than the Python one, am I?
have you declared the variable ‘line’?
for (row=0; row<ROWS; line++) // causes error.
full of error
For those who think the code above is full of errors: why don’t you just replace line with row :evil: !
this is neat, thanks.