A simple gaussian elimination implemented in C.
To simplify, I hard coded the linear system
| 10 x1 | + 2 x2 | + 3 x3 | + 4 x4 | = 5 | |
| 6 x1 | + 17 x2 | + 8 x3 | + 9 x4 | = 10 | |
| 11 x1 | + 12 x2 | + 23 x3 | + 14 x4 | = 15 | |
| 16 x1 | + 17 x2 | + 18 x3 | + 29 x4 | = 20 |
into the AB float matrix.
/*
* Description: Solve a hard coded linear system by gaussian elimination
* Author: Silveira Neto
* License: Public Domain
*/
#include
#include
#define ROWS 4
#define COLS 5
/**
* Linear System, Ax = B
*
* 10*x1 + 2*x2 + 3*x3 + 4*x4 = 5
* 6*x1 + 17*x2 + 8*x3 + 9*x4 = 10
* 11*x1 + 12*x2 + 23*x3 + 14*x4 = 15
* 16*x1 + 17*x2 + 18*x3 + 29*x4 = 20
*/
float AB[ROWS][COLS] = {
{10, 2, 3, 4, 5},
{ 6, 17, 8, 9, 10},
{11, 12, 23, 14, 15},
{16, 17, 18, 29, 20}
};
/* Answer x from Ax=B */
float X[ROWS] = {0,0,0,0};
int main(int argc, char** argv) {
int row, col, i;
/* gaussian elimination */
for (col=0; col
Before the gaugassian elimination, AB is
10 2 3 4 5
6 17 8 9 10
11 12 23 14 15
16 17 18 29 20
and after it is
10.00000 0.00000 0.00000 0.00000 2.82486
0.00000 15.80000 0.00000 0.00000 3.92768
0.00000 0.00000 15.85443 0.00000 3.85164
0.00000 0.00000 0.00000 14.13174 3.35329
that corresponds to
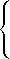
10 x1
= 2.82486
15.80000 x2
= 3.92768
15.85443 x3
= 3.85164
14.13174 x4
= 3.35329
The solution vector is X = (x1, x2, x3, x4). We get it by X=B/A.
The program output, X, is
0.28249 0.24859 0.24294 0.23729
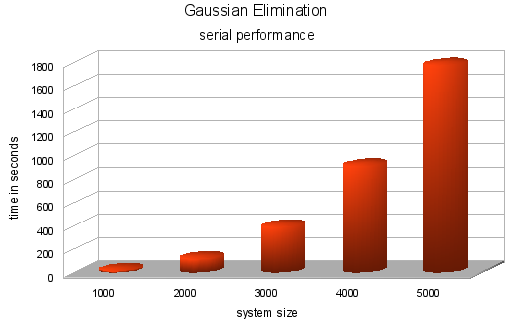
Benchmarking:
I'm this serial implementation over one node of our cluster, a machine with 4 processors (Intel Xeon 1.8 Ghz) and 1Gb RAM memory. I tried random systems from 1000 to 5000 variables and got the average time.